Understanding Interference and Diffraction: Similarities and Differences
Excellent Theory that will Give clarity on this Confusing Topic - Numerous Reasoning and Assertion questions included.
When studying the wave nature of light, two fundamental phenomena—interference and diffraction—frequently come into focus. Both play a critical role in understanding the behavior of waves, but they often confuse students because they seem so interconnected. In this blog, we’ll break down how interference and diffraction are similar, how they differ, and why they’re important in understanding wave physics.
How Are Interference and Diffraction Similar?
Wave Nature:
Both interference and diffraction arise due to the wave nature of light. These phenomena cannot be explained using the particle theory of light and are key evidence supporting the wave theory.Superposition Principle:
Both phenomena are governed by the principle of superposition, which states that when two or more waves overlap, their amplitudes combine algebraically.Formation of Patterns:
Both interference and diffraction result in the formation of patterns of alternating bright and dark regions. These patterns are created due to constructive interference (bright regions) and destructive interference (dark regions).Dependence on Wavelength:
Both phenomena are highly dependent on the wavelength of the wave. Changes in wavelength alter the spacing and intensity of the patterns.Applications:
Both are used in various practical applications, such as in optical instruments, spectroscopy, and the analysis of wave behavior.
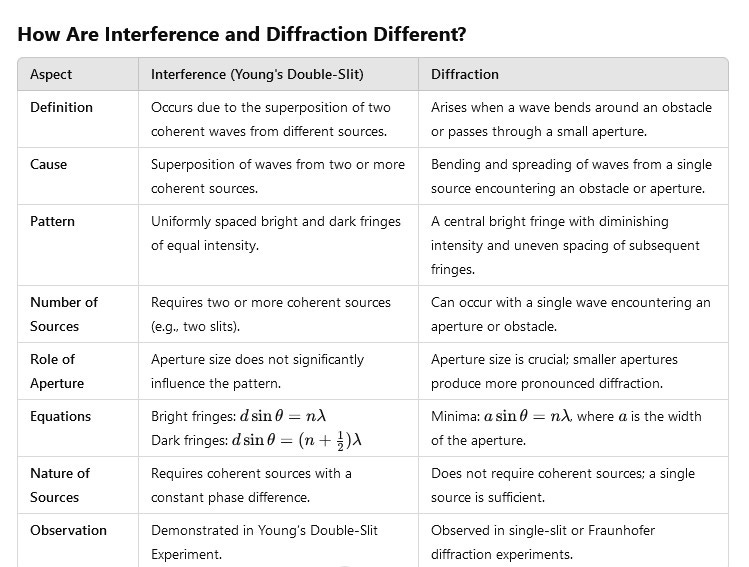
How Are Interference and Diffraction Different?
Visualizing Interference and Diffraction
Interference: Think of two pebbles dropped into a pond, creating overlapping ripple patterns. Where the ripples align, you see constructive interference, and where they cancel, you see destructive interference.
Diffraction: Imagine ocean waves passing through a narrow harbor opening and spreading out on the other side. The bending and spreading of the waves is diffraction.
How Are Diffraction and Interference Linked?
In many experiments, particularly in Young’s double-slit setup, we observe that the diffraction and interference patterns are intertwined. The overall observed pattern is actually a combination of the two phenomena:
Diffraction Enveloping Interference:
The bright and dark fringes of interference are modulated by the diffraction pattern. This means that the central bright region and subsequent fringes of the interference pattern are shaped by the intensity profile of the diffraction pattern. For example, in a double-slit experiment, the interference pattern consists of several evenly spaced bright and dark fringes, but their intensity decreases as you move outward, which is due to diffraction.Single-Slit Diffraction in Double-Slit Experiment:
In the double-slit experiment, each slit acts as a single source, and diffraction occurs at each slit. The diffraction pattern from each slit overlaps with the interference pattern created by the two slits, resulting in a combined pattern. The central bright fringe is the brightest due to constructive interference, while the side fringes diminish in intensity due to the diffraction envelope.Mathematical Relationship Between Intensity:
The intensity of the observed pattern is a product of two factors: the diffraction intensity and the interference intensity. Mathematically:I= Idiffraction× Iinterference.
Diffraction Intensity: This determines the broad envelope of the pattern and depends on the width of the aperture. For a single slit, the diffraction intensity follows: Idiffraction= I0 (sinβ/β)^2
Interference Intensity: This determines the fine structure within the diffraction envelope, arising from the path difference between the two slits. It is given by: Iinterference=I0 cos^2(πdsinθ/ λ), where d is the distance between the slits. The resulting intensity pattern shows interference fringes modulated by the overall diffraction envelope.
Practical Implications:
The interplay between interference and diffraction provides insights into the wave nature of light and helps measure key parameters like wavelength and slit width. For instance, analyzing the spacing of interference fringes and the diffraction envelope allows physicists to calculate the width of slits and other properties of the experimental setup.
Assertion and Reasoning Questions
Assertion (A): In Young's double-slit experiment, the central bright fringe is always the brightest.
Reason (R): The central bright fringe results from the longest path difference between the two slits.
Answer: (A) is true, but (R) is false. The central fringe is brightest due to maximum constructive interference, as all light waves combine in phase at the center, not because of the path difference.Assertion (A): Diffraction can occur even with a single wave source.
Reason (R): Diffraction arises due to the bending of waves around an obstacle or through a small aperture.
Answer: Both (A) and (R) are true, and (R) explains (A). Diffraction happens whenever waves encounter an obstacle or narrow opening, spreading into regions of geometric shadow.Assertion (A): A single-slit diffraction pattern shows a central bright fringe wider than the others.
Reason (R): The intensity of the central fringe is due to maximum constructive interference from all parts of the aperture.
Answer: Both (A) and (R) are true, and (R) explains (A). The central maximum occurs because light from all parts of the aperture constructively interferes at the center, producing the widest and brightest fringe.Assertion (A): Fringe spacing in interference depends only on the wavelength of light.
Reason (R): Fringe spacing is proportional to the wavelength and inversely proportional to slit separation.
Answer: (A) is false, but (R) is true. While wavelength affects fringe spacing, slit separation is equally critical; smaller slit spacing results in wider fringes.Assertion (A): The positions of diffraction minima are determined by the sine function of the angle.
Reason (R): Diffraction minima occur when light from different parts of the aperture cancels out.
Answer: Both (A) and (R) are true, and (R) explains (A). The condition for minima involves destructive interference of light waves, described by the sine function.Assertion (A): Interference patterns cannot be observed if the sources are not coherent.
Reason (R): Coherence ensures a constant phase difference, which is necessary for sustained interference.
Answer: Both (A) and (R) are true, and (R) explains (A). Coherent sources maintain a fixed phase relationship, crucial for the formation of stable interference patterns.Assertion (A): The intensity of the diffraction envelope modulates the brightness of interference fringes.
Reason (R): The observed pattern is a product of the diffraction intensity and interference intensity.
Answer: Both (A) and (R) are true, and (R) explains (A). The overall pattern combines the broad diffraction envelope with the finer interference fringes, modulating their brightness.Assertion (A): Increasing the slit separation in Young’s experiment reduces the fringe spacing.
Reason (R): Fringe spacing is inversely proportional to slit separation.
Answer: Both (A) and (R) are true, and (R) explains (A). As slit separation increases, the angular separation between adjacent fringes decreases, compressing the pattern.Assertion (A): Red light produces wider fringes than blue light in interference patterns.
Reason (R): Fringe spacing is directly proportional to the wavelength of light.
Answer: Both (A) and (R) are true, and (R) explains (A). Red light has a longer wavelength than blue light, resulting in larger fringe spacing in interference patterns.Assertion (A): In a diffraction pattern, the central maximum is the most intense.
Reason (R): All rays from the aperture contribute constructively at the central maximum.
Answer: Both (A) and (R) are true, and (R) explains (A). All light waves add constructively at the central maximum, leading to the highest intensity.
Conclusion
Both interference and diffraction reveal the fascinating properties of waves and provide insight into the behavior of light, sound, and even quantum particles. While they share similarities, their distinctions lie in their causes, patterns, and experimental setups. Mastering these concepts is essential for understanding advanced topics in physics, from wave optics to quantum mechanics.
By appreciating these phenomena, you’ll not only excel in your exams but also gain a deeper understanding of the wave nature of the universe. So next time you see a ripple in water or light through a slit, you’ll know the physics behind the magic!